Should we invert hypothesis tests to create confidence intervals
Since I have taught this topic in intro stat courses, I was interested to hear that Andrew Gelman does not think that inverting hypothesis tests is a generally valid means of obtaining confidence intervals. The crux of the matter is the graph:
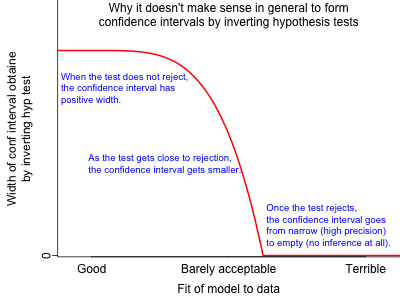Points where the red line is on the x-axis are points where the model does not fit the data and therefore it makes no sense to obtain a confidence interval for a parameter in an irrelevant model. This is no problem since the red line being on the x-axis means a zero-width confidence interval which would be very suspicious.
The main problem are points just left of where the red line meets the x-axis. These are points where the model fits the data poorly, but a confidence interval is incredibly narrow. So there is no indication that (from the confidence interval) that the model is poor and therefore it is tempting to believe the confidence interval is true (or has the correct coverage).
There is a lot of discussion about this post on Gelman's page, but one comment suggested that a Bayesian credible interval would have this same problem. Unfortunately Gelman's response does not address this central point. I would agree with the comment since the problem being reported is what happens when the model fits the data poorly.
Gelman's final comment is also a bit bizarre since he states ``inverting hypothesis tests is not a good general principle for obtaining interval estimates. You’re mixing up two ideas: inference within a model and checking the fit of a model.'' No, you are not mixing the two ideas since the hypothesis test that is used to create the confidence interval is still done within the model.
Bottom line: You should always do model checking prior to inference. If the model fits poorly, then the inference is most likely irrelevant.
blog comments powered by Disqus
Points where the red line is on the x-axis are points where the model does not fit the data and therefore it makes no sense to obtain a confidence interval for a parameter in an irrelevant model. This is no problem since the red line being on the x-axis means a zero-width confidence interval which would be very suspicious.
The main problem are points just left of where the red line meets the x-axis. These are points where the model fits the data poorly, but a confidence interval is incredibly narrow. So there is no indication that (from the confidence interval) that the model is poor and therefore it is tempting to believe the confidence interval is true (or has the correct coverage).
There is a lot of discussion about this post on Gelman's page, but one comment suggested that a Bayesian credible interval would have this same problem. Unfortunately Gelman's response does not address this central point. I would agree with the comment since the problem being reported is what happens when the model fits the data poorly.
Gelman's final comment is also a bit bizarre since he states ``inverting hypothesis tests is not a good general principle for obtaining interval estimates. You’re mixing up two ideas: inference within a model and checking the fit of a model.'' No, you are not mixing the two ideas since the hypothesis test that is used to create the confidence interval is still done within the model.
Bottom line: You should always do model checking prior to inference. If the model fits poorly, then the inference is most likely irrelevant.
blog comments powered by Disqus
Published
28 August 2011