Ridge regression

This is a quick demonstration of ridge regression in the context of a simple example constructed by Marquardt and Snee in their paper Ridge Regression in Practice. This example generates data from the model y = x1+x2+x3+e for a total of 8 observations. A tuning parameter, a, determines the amount of correlation between x1 and x2. In the example from the paper and duplicated here, a is set to 0.1, 0.5, and 0.9 which corresponds to a correlation between x1 and x2 of 0.110, 0.667, and 0.989, respectively.

The purpose of this post is to simply take a look at the ridge traces, i.e. the plot of parmeter estimates vs the ridge penalty parameter, lambda, to get some understanding of how the penalty affects the ridge estimates.

The function below just recreates the data set for a particular value of a.

df = function(a) {
    mu = rep(1, 8)
    x1 = c(-1, 1, -1, 1, -1, 1, -(1 - 2 * a), (1 - 2 * a))
    x2 = c(-1, 1, -1, 1, (1 - 2 * a), -(1 - 2 * a), 1, -1)
    x3 = c(-1, -1, 1, 1, -1, -1, 1, 1)
    Ey = x1 + x2 + x3
    
    e = c(-0.305, -0.321, 1.9, -0.778, 6.17, -1.43, 0.267, 0.978)
    y = Ey + e
    return(data.frame(mu = mu, x1 = x1, x2 = x2, x3 = x3, Ey = Ey, e = e, y = y))
}

The plots below show the traces for the three values of a for the penalty parameter in the range 0 to 1.

library(MASS)
par(mfrow = c(1, 3))

ylm = 10
plot(lm.ridge(y ~ x1 + x2 + x3, df(0.1), lambda = seq(0, 1, 0.01)), main = "a=0.1", 
    ylim = c(-ylm, ylm))
legend("topright", c("x1", "x2", "x3"), col = 1:3, lty = 1:3)

plot(lm.ridge(y ~ x1 + x2 + x3, df(0.5), lambda = seq(0, 1, 0.01)), main = "a=0.5", 
    ylim = c(-ylm, ylm))
legend("topright", c("x1", "x2", "x3"), col = 1:3, lty = 1:3)

plot(lm.ridge(y ~ x1 + x2 + x3, df(0.9), lambda = seq(0, 1, 0.01)), main = "a=0.9", 
    ylim = c(-ylm, ylm))
legend("topright", c("x1", "x2", "x3"), col = 1:3, lty = 1:3)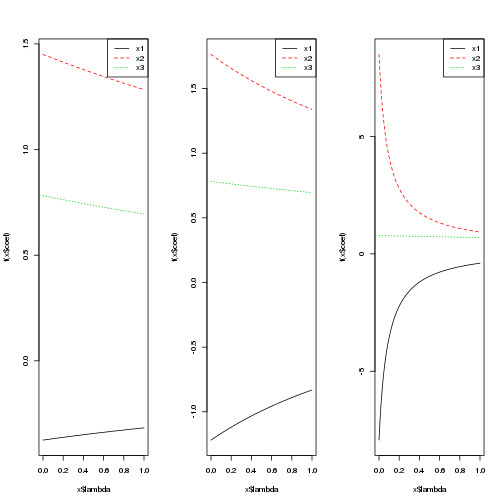

center

Unfortunately the ylim argument is having no impact, so the plots are not as comparable as I’d like. The y-axis ranges from -1.5 to 1.5 for a=0.1, from -2 to 2 for a=0.5, and -10 to 10 for a=0.9. At lambda=0, we obtain the least squares estimates. As lambda increases, we shrink these estimates back toward zero. The correlation between x1 and x2 is apparent in the estimates because x2 is larger than 1 (the truth) and x1 is negative.

The lm.ridge function also has the ability to select the penalty according to some criterion.

select(lm.ridge(y ~ x1 + x2 + x3, df(0.1), lambda = seq(0, 20, 1e-04)))

## modified HKB estimator is 2.187 
## modified L-W estimator is 2.283 
## smallest value of GCV  at 18.22

select(lm.ridge(y ~ x1 + x2 + x3, df(0.5), lambda = seq(0, 10, 1e-04)))

## modified HKB estimator is 0.8962 
## modified L-W estimator is 1.993 
## smallest value of GCV  at 10

select(lm.ridge(y ~ x1 + x2 + x3, df(0.9), lambda = seq(0, 10, 1e-04)))

## modified HKB estimator is 0.02534 
## modified L-W estimator is 1.425 
## smallest value of GCV  at 0.0275

These results are certainly not consistent across the different methods of selecting the penalty. The generalized cross validation approach (GCV) always chooses the right endpoint even up to 1000 for a=0.5.

For another example of the ridge traces, we look at the example from the lm.ridge function.

longley  # not the same as the S-PLUS dataset

##      GNP.deflator   GNP Unemployed Armed.Forces Population Year Employed
## 1947         83.0 234.3      235.6        159.0      107.6 1947    60.32
## 1948         88.5 259.4      232.5        145.6      108.6 1948    61.12
## 1949         88.2 258.1      368.2        161.6      109.8 1949    60.17
## 1950         89.5 284.6      335.1        165.0      110.9 1950    61.19
## 1951         96.2 329.0      209.9        309.9      112.1 1951    63.22
## 1952         98.1 347.0      193.2        359.4      113.3 1952    63.64
## 1953         99.0 365.4      187.0        354.7      115.1 1953    64.99
## 1954        100.0 363.1      357.8        335.0      116.2 1954    63.76
## 1955        101.2 397.5      290.4        304.8      117.4 1955    66.02
## 1956        104.6 419.2      282.2        285.7      118.7 1956    67.86
## 1957        108.4 442.8      293.6        279.8      120.4 1957    68.17
## 1958        110.8 444.5      468.1        263.7      122.0 1958    66.51
## 1959        112.6 482.7      381.3        255.2      123.4 1959    68.66
## 1960        114.2 502.6      393.1        251.4      125.4 1960    69.56
## 1961        115.7 518.2      480.6        257.2      127.9 1961    69.33
## 1962        116.9 554.9      400.7        282.7      130.1 1962    70.55

names(longley)[1] <- "y"
lm.ridge(y ~ ., longley)

##                       GNP   Unemployed Armed.Forces   Population 
##   2946.85636      0.26353      0.03648      0.01116     -1.73703 
##         Year     Employed 
##     -1.41880      0.23129

par(mfrow = c(1, 1))
plot(lm.ridge(y ~ ., longley, lambda = seq(0, 0.1, 0.001)))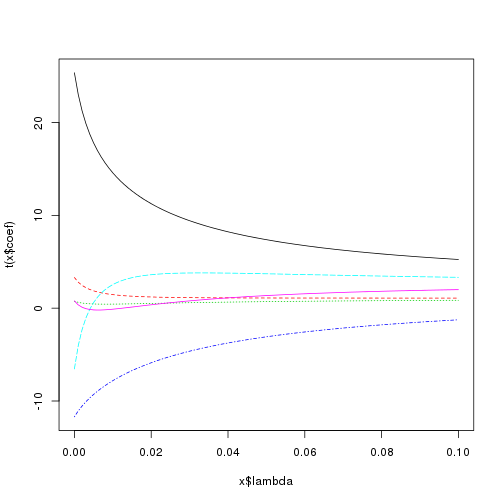

center

select(lm.ridge(y ~ ., longley, lambda = seq(0, 0.1, 1e-04)))

## modified HKB estimator is 0.006837 
## modified L-W estimator is 0.05267 
## smallest value of GCV  at 0.0057

The main comment here is to note that the shrinkage is not monotonic for each individual variable. Notice the pink line starts above zero, then decreases below zero for small penalties, but then increase above zero and surpasses its least squares estimate. Similarly the light blue line starts at a relatively large negative value and then increases to a somewhat large positive value.

blog comments powered by Disqus

Published

05 September 2013

Exploration of ridge regression

Ridge regression

Published

Tags