DLM MCMC
This post looks at the autocorrelation in a simple DLM when using JAGS, which samples each state individually, and FFBS, which samples the states jointly. This is put within the context of a local level model with unknown observation and evolution variance.
Simulate the data
require(methods, quietly=TRUE)
require(dlm, quietly=TRUE)##
## Attaching package: 'dlm'## The following object is masked from 'package:ggplot2':
##
## %+%require(rjags, quietly=TRUE)## Warning in library(package, lib.loc = lib.loc, character.only = TRUE,
## logical.return = TRUE, : there is no package called 'rjags'# Simulate data
ll = dlmModPoly(1, dV=1, dW=.01, m0=0, C0=1)
o = dlmForecast(ll, 100, sampleNew=1)Fit the model using JAGS (the model looks terrible, but it should work).
jags_ll = "
model {
for (i in 2:n) {
y[i-1] ~ dnorm(theta[i], tauV)
theta[i] ~ dnorm(theta[i-1], tauW)
}
theta[1] ~ dnorm(0,1)
tauV ~ dgamma(1,1)
tauW ~ dgamma(1,1)
}
"
dat = list(y=as.numeric(o$newObs[[1]]))
dat$n = length(dat$y)+1
m = jags.model(textConnection(jags_ll), dat,
n.adapt=2000)## Error in jags.model(textConnection(jags_ll), dat, n.adapt = 2000): could not find function "jags.model"res = coda.samples(m, c("tauV", "tauW","theta"), n.iter=2000)## Error in coda.samples(m, c("tauV", "tauW", "theta"), n.iter = 2000): could not find function "coda.samples"Fit the model using the dlm package in R.
joint = dlmGibbsDIG(o$newObs[[1]], ll,
a.y=1, b.y=1,
a.theta=1, b.theta=1,
n.sample=1000, thin=1)##
|
| | 0%
|
| | 1%
|
|= | 1%
|
|= | 2%
|
|== | 2%
|
|== | 3%
|
|== | 4%
|
|=== | 4%
|
|=== | 5%
|
|==== | 5%
|
|==== | 6%
|
|==== | 7%
|
|===== | 7%
|
|===== | 8%
|
|====== | 8%
|
|====== | 9%
|
|====== | 10%
|
|======= | 10%
|
|======= | 11%
|
|======= | 12%
|
|======== | 12%
|
|======== | 13%
|
|========= | 13%
|
|========= | 14%
|
|========= | 15%
|
|========== | 15%
|
|========== | 16%
|
|=========== | 16%
|
|=========== | 17%
|
|=========== | 18%
|
|============ | 18%
|
|============ | 19%
|
|============= | 19%
|
|============= | 20%
|
|============= | 21%
|
|============== | 21%
|
|============== | 22%
|
|=============== | 22%
|
|=============== | 23%
|
|=============== | 24%
|
|================ | 24%
|
|================ | 25%
|
|================= | 25%
|
|================= | 26%
|
|================= | 27%
|
|================== | 27%
|
|================== | 28%
|
|=================== | 28%
|
|=================== | 29%
|
|=================== | 30%
|
|==================== | 30%
|
|==================== | 31%
|
|==================== | 32%
|
|===================== | 32%
|
|===================== | 33%
|
|====================== | 33%
|
|====================== | 34%
|
|====================== | 35%
|
|======================= | 35%
|
|======================= | 36%
|
|======================== | 36%
|
|======================== | 37%
|
|======================== | 38%
|
|========================= | 38%
|
|========================= | 39%
|
|========================== | 39%
|
|========================== | 40%
|
|========================== | 41%
|
|=========================== | 41%
|
|=========================== | 42%
|
|============================ | 42%
|
|============================ | 43%
|
|============================ | 44%
|
|============================= | 44%
|
|============================= | 45%
|
|============================== | 45%
|
|============================== | 46%
|
|============================== | 47%
|
|=============================== | 47%
|
|=============================== | 48%
|
|================================ | 48%
|
|================================ | 49%
|
|================================ | 50%
|
|================================= | 50%
|
|================================= | 51%
|
|================================= | 52%
|
|================================== | 52%
|
|================================== | 53%
|
|=================================== | 53%
|
|=================================== | 54%
|
|=================================== | 55%
|
|==================================== | 55%
|
|==================================== | 56%
|
|===================================== | 56%
|
|===================================== | 57%
|
|===================================== | 58%
|
|====================================== | 58%
|
|====================================== | 59%
|
|======================================= | 59%
|
|======================================= | 60%
|
|======================================= | 61%
|
|======================================== | 61%
|
|======================================== | 62%
|
|========================================= | 62%
|
|========================================= | 63%
|
|========================================= | 64%
|
|========================================== | 64%
|
|========================================== | 65%
|
|=========================================== | 65%
|
|=========================================== | 66%
|
|=========================================== | 67%
|
|============================================ | 67%
|
|============================================ | 68%
|
|============================================= | 68%
|
|============================================= | 69%
|
|============================================= | 70%
|
|============================================== | 70%
|
|============================================== | 71%
|
|============================================== | 72%
|
|=============================================== | 72%
|
|=============================================== | 73%
|
|================================================ | 73%
|
|================================================ | 74%
|
|================================================ | 75%
|
|================================================= | 75%
|
|================================================= | 76%
|
|================================================== | 76%
|
|================================================== | 77%
|
|================================================== | 78%
|
|=================================================== | 78%
|
|=================================================== | 79%
|
|==================================================== | 79%
|
|==================================================== | 80%
|
|==================================================== | 81%
|
|===================================================== | 81%
|
|===================================================== | 82%
|
|====================================================== | 82%
|
|====================================================== | 83%
|
|====================================================== | 84%
|
|======================================================= | 84%
|
|======================================================= | 85%
|
|======================================================== | 85%
|
|======================================================== | 86%
|
|======================================================== | 87%
|
|========================================================= | 87%
|
|========================================================= | 88%
|
|========================================================== | 88%
|
|========================================================== | 89%
|
|========================================================== | 90%
|
|=========================================================== | 90%
|
|=========================================================== | 91%
|
|=========================================================== | 92%
|
|============================================================ | 92%
|
|============================================================ | 93%
|
|============================================================= | 93%
|
|============================================================= | 94%
|
|============================================================= | 95%
|
|============================================================== | 95%
|
|============================================================== | 96%
|
|=============================================================== | 96%
|
|=============================================================== | 97%
|
|=============================================================== | 98%
|
|================================================================ | 98%
|
|================================================================ | 99%
|
|=================================================================| 99%
|
|=================================================================| 100%Plot traceplots and autocorrelation for the middle state.
par(mfrow=c(2,2))
plot(as.numeric(res[[1]][1001:2000,52]), type="l")## Error in plot(as.numeric(res[[1]][1001:2000, 52]), type = "l"): object 'res' not foundacf(res[[1]][,52])## Error in as.ts(x): object 'res' not foundplot(joint$theta[52,1,],type="l")
acf(joint$theta[52,1,])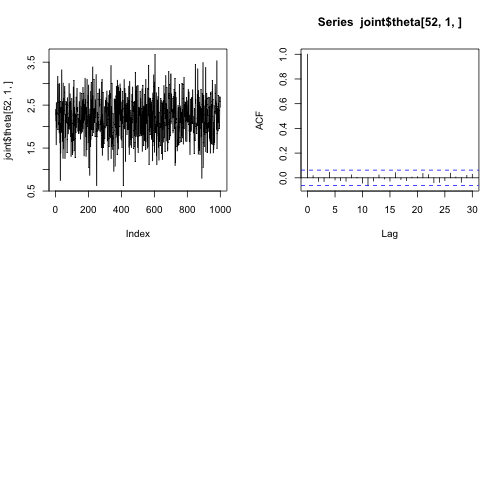
The elephant in the room here is in the implementation since the JAGS code runs quite a bit faster than the dlm code. Of course, the dlm code is written to handle much more complicated DLMs.
blog comments powered by Disqus