Jarad Niemi

Rejection sampling

Here is a quick example of rejection sampling with the example coming almost verbatim from Robert and Casella. Suppose f(x) is our target distribution and q(x) is our proposal distribution. Given an M such that f(x) <= M q(x) for all x, rejection sampling samples a value x from q(x) and U~Unif(0,1) and accepts it if U <= f(x)/M q(x). The probability of acceptance is 1/M.

In this example, we have a Beta(a,b) as our target distribution and the proposal distribution is Unif(0.1). The M that attains the above inequality is simply the density of the Beta(a,b) at its mode. Since the mode is c=(a-1)/(a+b-2), M = Beta(c;a,b).

Set up the targt and proposal densities.

a = 5
b = 12
target = function(x) dbeta(x,a,b)
proposal = dunif

Calculate M and the probability of acceptance.

mode = (a-1)/(a+b-2)
M = target(mode)
1/M
## [1] 0.2745091

Perform rejection sampling

n = 1000
points = runif(n)
uniforms = runif(n)
accept = uniforms < (target(points)/(M*proposal(points)))

The plot below has target (red) and proposal (green) density as well as the proposal density scaled by M (green, dashed) to show how it creates an envelope over the target. The points are accepted (blue circle) and rejected (red x) values on the x-axis with their associated uniform draws on the y-axis.

curve(target, lwd=2)
curve(proposal, add=TRUE, col="seagreen", lwd=2)
curve(M*proposal(x), add=TRUE, col="seagreen", lty=2, lwd=2)
points(points, M*uniforms, pch=ifelse(accept,1,4), col=ifelse(accept,"blue","red"), lwd=2)
legend("topright", c("target","proposal","accepted","rejected"), 
       lwd=c(2,2,NA,NA), col=c("black","seagreen","blue","red"),
       pch=c(NA,NA,1,4), bg="white")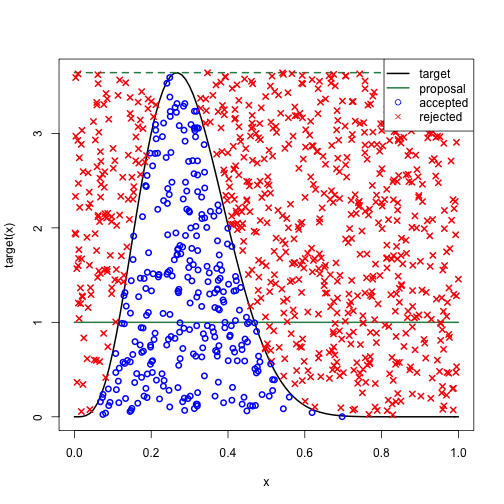

center

The empirical acceptance probability is.

sum(accept)/n
## [1] 0.291
blog comments powered by Disqus

Published

03 October 2013

Tags