Slice sampling for multimodal targets
Previously, I looked at some simple slice sampling algorithms that were appropriate for unimodal posteriors. Here are some more general slice sampling algortihms based on the Slice sampling paper from Neal (2003). The two algorithms here are the stepping-out and doubling samplers.
Stepping-out slice sampler
The idea here is to build an interval around the currently sampled value and then sample uniformly in the interval until a sample is obtained where the target evaluated at the proposed value is larger than the slice auxiliary variable. There is a tuning parameter w that is the initial interval width and the interval is constructed by
- Randomly placing the interval over the current value.
- Stepping out from the L and R endpoints of the interval until the target is lower than the slice.
The maximum number of steps taken can be controlled.
slice = function(n,init_x,target,w,max_steps) {
u = x = rep(NA,n)
x[1] = init_x
for (i in 2:n) {
u[i] = runif(1,0,target(x[i-1]))
L = x[i-1] - runif(1,0,w)
R = L+w
# Step out
J = floor(max_steps*runif(1))
K = (max_steps-1)-J
while((u[i]<target(L)) & J>0) {
L = L-w
J = J-1
}
while((u[i]<target(R)) & K>0) {
R = R+w
K = K-1
}
# Sample and shrink
repeat {
x[i] = runif(1,L,R)
if (u[i]<target(x[i])) break
# shrink
if (x[i]>x[i-1]) R = x[i]
if (x[i]<x[i-1]) L = x[i]
}
}
return(list(x=x,u=u))
}target = function(x) dnorm(x,-2)/2+dnorm(x,2)/2
res = slice(1e4, 0, target, 1, 10)
hist(res$x,freq=F,100)
curve(target, add=TRUE)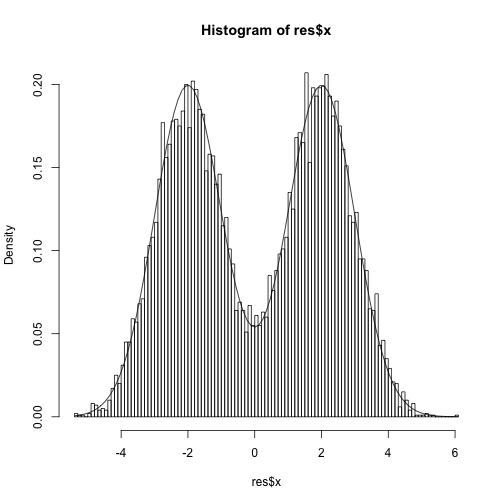
Doubling slice sampler
The doubling slice sampler has the same idea except that rather than adding a fixed width to the interval every time, the width of the interval is doubled in size either to the right or to the left. Given the tuning parameter w that determines the original interval width, the interval is constructed by
- Randomly placing the interval over the current value.
- Doubling the size of the interval randomly to either the right or left until both sides have the target less than the slice variable.
The maximum number of doublings can be controlled.
The doubling procedure can be more efficient if w was chosen too small as it attains a larger interval in the same number of steps. This efficiency comes at the cost of an additional check when trying to accept a proposed value. From the manuscript
This procedure works backward through the intervals that the doubling procedure would pass through to arrive at [the doubled interval] when starting from the new point, checking that none of [the intermediate intervals] has both ends outside the slice, which would lead to earlier termination of the doubling procedure.
The function to perform this check is ‘accept’.
accept = function(x0, x1, L, R, u, w) {
D = FALSE
while(R-L > 1.1*w) {
M = (L+R)/2
if ((x0 < M & x1 >= M) | (x0 >= M & x1 < M)) D = TRUE
if (x1 < M) { R = M } else { L = M }
if (D & u>=target(L) & u>= target(R)) {
return(FALSE)
}
}
return(TRUE)
}Now, we have the doubling slice sampler which looks very similar to the stepping-out slice sampler.
slice = function(n,init_x,target,w,max_doubling) {
u = x = rep(NA,n)
x[1] = init_x
for (i in 2:n) {
u[i] = runif(1,0,target(x[i-1]))
L = x[i-1] - runif(1,0,w)
R = L+w
# Step out
K = max_doubling
while((u[i]<target(L) | u[i]<target(R)) & K>0) {
if (runif(1) < 0.5) {
L = L-(R-L)
} else {
R = R+(R-L)
}
K = K-1
}
# Sample and shrink
repeat {
x[i] = runif(1,L,R)
if (u[i]<target(x[i]) &
accept(x[i-1], x[i], L, R, u[i], w)) break
# shrink
if (x[i]>x[i-1]) R = x[i]
if (x[i]<x[i-1]) L = x[i]
}
}
return(list(x=x,u=u))
}target = function(x) dnorm(x,-2)/2+dnorm(x,2)/2
res = slice(1e4, 0, target,1, 10)
hist(res$x,freq=F,100)
curve(target, add=TRUE)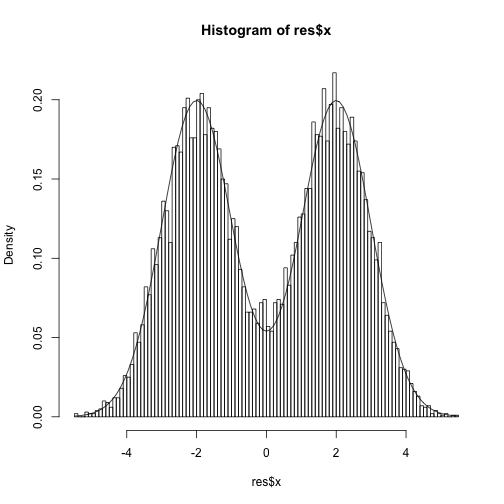
blog comments powered by Disqus